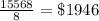Question

Eric’s average income for the first 4 months of the year is $1,450.25, what must be his

average income for the remaining 8 months so that his average income for the year is
$1,780.75?

Answer 1

Average income of Eric for the remaining 8 months =
`\$1946`

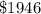
Explanation:

Given: Average income of Eric for the first 4 months of the year is equal to $1,450.25

To find: average income for the remaining 8 months so that his average income for the year is $1,780.75

Solution:

Average income = Total income for the year/Total number of months

Average income of Eric for the first 4 months = $1,450.25

So,

Total income of Eric for the first 4 months = 1,450.25 × 4 = 5801

Let x denotes total income of Eric for the remaining 8 months

Total income for the year = 5801 + x

Therefore,

Average income for the year =
`(5801+x)/(12)`

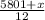
Also, average income for the year is $1,780.75

`1780.75=(5801+x)/(12)\\1780.75* 12=5801+x\\21369=5801+x\\21369-5801=x\\15568=x`

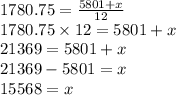
Total income of Eric for the remaining 8 months = $15568

Average income of Eric for the remaining 8 months =
`(15568)/(8)=\$1946`