Answer:
$1946
Explanation:
Eric’s average income for the first 4 months of the year is $1,450.25
Therefore, his total earning in the first four months
= 4 X $1,450.25
=$5,801
Let the average income for the remaining 8 months= x
Then:
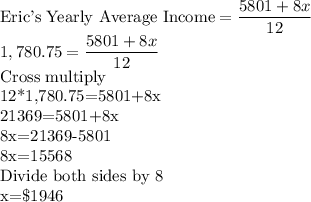
Therefore, to get an average income for the year of $1,780.75, Eric must earn an average income of $1946 for the remaining 8 months.