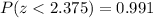Answer:
a)
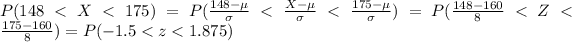
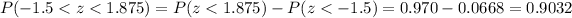
b)
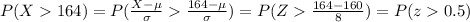
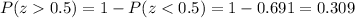
c)
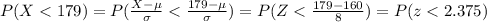
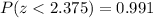
Explanation:
Let X the random variable that represent the heights of Guinean travels , and for this case we know the distribution for X is given by:
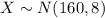
Where
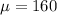 and
and
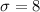
Part a
We are interested on this probability
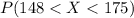
We can ue the z score formula given by:
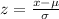
Using this formula we got:
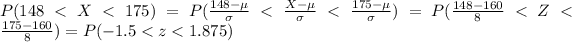
And we can find this probability with this difference using the normal standard distribution or excel:
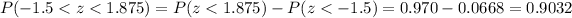
Part b
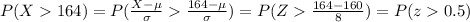
And we can find this probability with this difference using the normal standard distribution or excel:
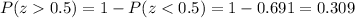
Part c
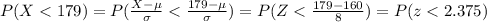
And we can find this probability with this difference using the normal standard distribution or excel: