Question

The members of a men’s club have a choice of wearing black or red vests to their club meetings. A study done over a period of many years determined that the percentage of black vests worn is 70%. If there are 10 men at a club meeting on a given night, what is the probability, to the nearest thousandth, that at least 8 of the vests worn will be black?

Answer 1

The probability that at least 8 of the vest worn will be black is 0.75490

Explanation:

The parameters given are;

The percentage of black vest worn = 70%, p₀ = 0.7

Number of men in sample, n = 10

Required number of men who wore black = 8

Proportion of sample
`\hat p` = 8/10 = 0.8

The z score of a proportion is given by the relation;

`z = \frac{\hat p - p_0}{\sqrt{(p_0(1 - p_0))/(n) } }`

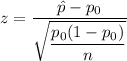
Plugging in the vales, we have;

`z = \frac{0.8 - 0.7}{\sqrt{(0.7(1 - 0.7))/(10) } } = 0.69`

From the z table we have probability = p(z < 0.69) = 0.75490

The probability that at least 8 of the vest worn will be black = 0.75490.

Answer 2

Explanation:

Let x be a random variable representing the number of the members of a men’s club that wear black vests to their club meetings. This is a binomial distribution since the outcomes are two ways. It is either they wear black or red. The probability of success, p = 70/100 = 0.7

The probability of failure, q would be 1 - p = 1 - 0.7 = 0.3

a) Number of samples, n = 10

We want to determine P(x ≤ 8)

From the binomial distribution calculator,

P(x ≤ 8) = 0.851