Question

According to a survey done at your school, about 42% of all the female students participate in 2 sport seasons. You randomly ask 5 female students at your school how many sport seasons they participate in. What is the probability that at least 3 of the 5 female students surveyed participate in 2 sport seasons? Show your work.

Answer 1

Answer: 0.353

Explanation:

We know that 42% of all the female students participate in 2 sports this season. (58% is the percent that did not)

This means that if we select a random student, there is a 0.42 probability that the student did participate in 2 sports this season.

Other thing that i will use is that, if we have a group of N objects, and we want to create a group of K objects out of the N, the number of combinations is:

`c = (N!)/((N - K)!*K!)`

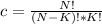
Now, out of 5, we want to find the proability that, at least 3 of them, did participate in at least 2 sports this season.

The probability that all 5 of them participated, is equal to the product of the individual probabilities. (so N = 5, and K = 5)

P = (0.42^5)*1 = 0.013

Now, if only 4 of them did participate (N = 5, k = 4), the probability is equal to:

P = (0.42^4)*(0.58)*5!/4! = (0.42^4)*(0.58)*5 = 0.09

The probability for only 3 is: (N = 5 and K = 3)

P = (0.42^3)*(0.58^2)*5!/(3!*2!) = (0.42^3)*(0.58^2)*(5*4/2) = 0.25

Then the total probability is:

P = 0.013 + 0.09 + 0.25 = 0.353