The key thing to look for to determine whether a sequence is geometric is to see whether the ratio between consecutive terms - the number I would multiply one term by to get the next - is constant.
By inspection, we see that the fourth answer choice satisfies that, as
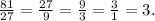Why not the first? We have
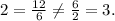
The third choice is not a geometric sequence, but rather an arithmetic sequence, where the difference between consecutive terms is constant. Just to make sure that it isn't geometric, we compute
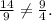
The second sequence is not geometric (although it does eventually converge to 1, but not its corresponding series), as
