Question

Given f(x) =x^2 -10x+22 what is the domain of f

Answer 1

d

Explanation:

i just got it right.:)

Answer 2

`f(x) = x^2 -10x +22`

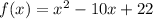
And we want to find the domain. And that represent the possible values for x. Since we have a quadratic function we have that the domain would be all the reals, and we can write:

`D= [x \in R]`

Where D represent the domain and R the set of the real numbers.

Explanation:

For this case we have the following function:

`f(x) = x^2 -10x +22`

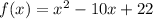
And we want to find the domain. And that represent the possible values for x. Since we have a quadratic function we have that the domain would be all the reals, and we can write:

`D= [x \in R]`

Where D represent the domain and R the set of the real numbers.