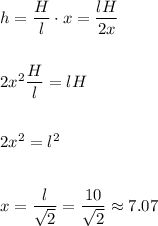Answer:
x = 10/√2 ≈ 7.07
Explanation:
Comenzaremos por dividir el triángulo en dos partes y definir H, como en la figura adjunta.
Aplicando el teorema de Tales, sabemos que:
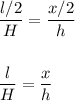
También sabemos que, dado que el tirángulo menor es la mitad que el triángulo mayor, la relación entre áreas es:
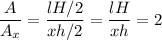
Dado que formamos dos triángulos rectángulos, podemos despejar el valor de H como:
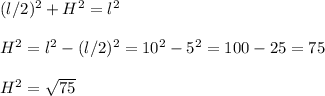
Podemos entonces despejar x de la siguiente manera: