Answer:
There are two possibilities:
 and
and
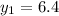
 and
and

Explanation:
Mathematically speaking, the statement is equivalent to this 2-variable non-linear system:

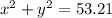
First,
 is cleared in the first equation:
is cleared in the first equation:
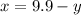
Now, the variable is substituted in the second one:
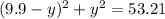
And some algebra is done in order to simplify the expression:
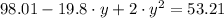
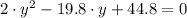
Roots are found by means of the General Equation for Second-Order Polynomials:
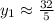 and
and
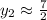
There are two different values for
 :
:
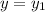
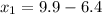

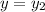


There are two possibilities:
 and
and
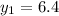
 and
and
