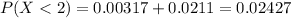Answer:
i)
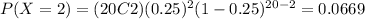
ii)


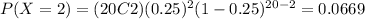
And replacing we got:
![P(X \geq 3) = 1- [0.00317+0.0211+0.0669]= 0.90883](https://img.qammunity.org/2021/formulas/mathematics/college/9qq19ft1m75clcxlj7j95u21k6op4hp05k.png)
iii)
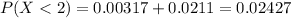
Explanation:
Let X the random variable of interest "number of inhabitants of a community favour a political party', on this case we now that:
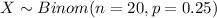
The probability mass function for the Binomial distribution is given as:
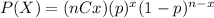
Where (nCx) means combinatory and it's given by this formula:
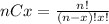
Part i
We want this probability:
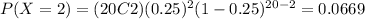
Part ii
We want this probability:

And we can use the complement rule and we have:
![P(X\geq 3) = 1-P(X<3)= 1-P(X \leq 2) =1- [P(X=0) +P(X=1) +P(X=2)]](https://img.qammunity.org/2021/formulas/mathematics/college/23qt8qz6bzu4d2bbrp675ba5vcwxo41qzi.png)
And if we find the individual probabilites we got:


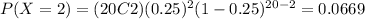
And replacing we got:
![P(X \geq 3) = 1- [0.00317+0.0211+0.0669]= 0.90883](https://img.qammunity.org/2021/formulas/mathematics/college/9qq19ft1m75clcxlj7j95u21k6op4hp05k.png)
Part iii
We want this probability:
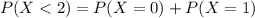
And replacing we got: