Answer:
b)
i) Focus ( 0,a) =
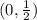
ii) The equation of the directrix is
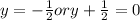
Explanation:
Step(i):-
A parabola is the set of all points in a plane that are equidistant from a fixed line and a fixed point (not in a line) in the plane
• The Fixed line is called the directrix of the parabola.
• The Fixed point is called the focus of the parabola.
• A line through the focus and perpendicular to the directrix is called the axis of the parabola.
• The point of intersection of parabola with the axis is called the vertex of the parabola.
Given Parabola x² = 2 y
Comparing x² = 4 a y
4 a = 2
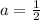
Focus ( 0,a) =
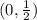
Step(ii)
The equation of the directrix is y = -a or y +a=0
The equation of the directrix is
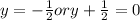
The equation of the directrix is 2 y +1 =0