Question

Consider xdy = 3ydx.

(a) Apply Theorem 1 and show the equation has unique solution in xy-plane where x 6= 0
(b) Theorem 1 will be inconclusive about existence and uniqueness of solution where x = 0 (that is on y-axis). For points on the y-axis (i) Show there are infinitely many different solutions for xdy = 3ydx y(0) = 0. (ii) Show there is no solution for xdy = 3ydx y(0) = b b != 0.

Answer 1

Question:

Consider xdy = 3ydx.

(a) Apply Theorem 1 and show the equation has unique solution in xy-plane where x ≠ 0

(b) Theorem 1 will be inconclusive about existence and uniqueness of solution where x = 0 (that is on y-axis). For points on the y-axis (i) Show there are infinitely many different solutions for xdy = 3ydx y(0) = 0. (ii) Show there is no solution for xdy = 3ydx,

y(0) = b, b ≠0.

Theorem 1 is attached.

Answer:

Given:

xdy = 3ydx

a) Given theorem 1 :

dy/dx = f (x, y)

we have:

`f(x, y) = (3y)/(x)`

`(d)/(dy) f(x, y) = (3)/(x)`

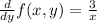
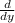`(d)/(dy)` is at interior of all angles except at point x=0.

Therefore for x≠0

`(d)/(dy) f(x, y) = (3)/(2)`

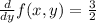
Thus, from theorem 1, there is a unique solution in the xy plane where x≠0

b) i) xdy = 3ydx y(0) = 0

We have:

`(dy)/(y) = (3)/(x) dx`

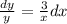
Integrating, we have:

∫
`(dy)/(y)` =∫
`(3)/(x) dx`

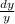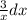
ln y = 3lnx + lnC

y = Cx³

Hence, y(0)=0 is satisfied for all values of C

Thus, there are infinitely many solutions for xdy = 3ydx

ii) xdy = 3ydx

y(0) = b, b ≠ 0.

From our part (i) above, we already know that, y = Cx³

Let's now take initial value of y as b,

ie, y(0) = b

b = 0

From the question, b≠0.

Thus, it means it has no solution.