Answer:
The correct answer is A.
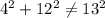
Explanation:
A right angled triangle is the type of triangle in which one of the three angles is
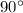 .
.
For a triangle to be right angled triangle, following equation must hold:
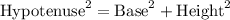
Where Hypotenuse is the largest side of triangle and is opposite to the angle with value
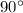 .
.
Base and Height are the two other sides making an angle of
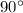 with each other.
with each other.
In the given question figure, largest side, XY = 13 units
Other two sides are:
YZ = 4 units
XZ = 12 units
For this
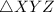 to be right angled, the following must be true:
to be right angled, the following must be true:
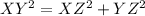
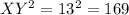
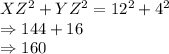

Hence, the given triangle is not a right angled triangle because of following:
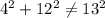
Hence, option A. is correct answer.