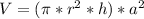Answer:
See explanation
Explanation:
Solution:-
- We will use the basic formulas for calculating the volumes of two solid bodies.
- The volume of a cylinder ( V_l ) is represented by:

- Similarly, the volume of cone ( V_c ) is represented by:
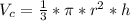
Where,
r : The radius of cylinder / radius of circular base of the cone
h : The height of the cylinder / cone
- We will investigate the correlation between the volume of each of the two bodies wit the radius ( r ). We will assume that the height of cylinder/cone as a constant.
- We will represent a proportionality of Volume ( V ) with respect to ( r ):
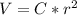
Where,
C: The constant of proportionality
- Hence the proportional relation is expressed as:
V∝ r^2
- The volume ( V ) is proportional to the square of the radius. Now we will see the effect of multiplying the radius ( r ) with a positive number ( a ) on the volume of either of the two bodies:

- Hence, we see a general rule frm above relation that multiplying the result by square of the multiple ( a^2 ) will give us the equivalent result as multiplying a multiple ( a ) with radius ( r ).
- Hence, the relations for each of the two bodies becomes:
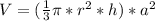
&