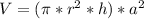Question

1. Determine a rule that could be used to explain how the volume of a

Cylinder or cone is affected when the radius is multiplied by a positive

number.

Answer 1

See explanation

Explanation:

Solution:-

- We will use the basic formulas for calculating the volumes of two solid bodies.

- The volume of a cylinder ( V_l ) is represented by:

`V_c = \pi *r^2*h`

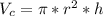
- Similarly, the volume of cone ( V_c ) is represented by:

`V_c = (1)/(3)*\pi *r^2 * h`

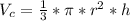
Where,

r : The radius of cylinder / radius of circular base of the cone

h : The height of the cylinder / cone

- We will investigate the correlation between the volume of each of the two bodies wit the radius ( r ). We will assume that the height of cylinder/cone as a constant.

- We will represent a proportionality of Volume ( V ) with respect to ( r ):

`V = C*r^2`

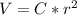
Where,

C: The constant of proportionality

- Hence the proportional relation is expressed as:

V∝ r^2

- The volume ( V ) is proportional to the square of the radius. Now we will see the effect of multiplying the radius ( r ) with a positive number ( a ) on the volume of either of the two bodies:

`V = C*(a*r)^2\\\\V = C*a^2*r^2`

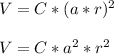
- Hence, we see a general rule frm above relation that multiplying the result by square of the multiple ( a^2 ) will give us the equivalent result as multiplying a multiple ( a ) with radius ( r ).

- Hence, the relations for each of the two bodies becomes:

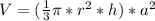
`V = ((1)/(3) \pi *r^2*h)*a^2`

&

`V = ( \pi *r^2*h)*a^2`