Question

14. Roger is on a playground swing, and he is swinging back and forth in such a way that the height, h, in feet, of the swing off the ground is given by the equation h=3cos(3π/2t) +5, where t is in seconds. How many seconds elapses between two consecutive times that the swing is at its maximum height?​

Answer 1

The time
`t = (3)/(2)` seconds elapses between two consecutive times that the swing is at its maximum height 'h' = 2

Explanation:

Explanation:-

Step(i):-

Given function
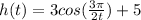`h(t) = 3 cos ((3\pi )/(2 t) ) +5` ....(i)

By using derivative formulas

`(d cosx )/(d x) = -sinx`

`(d x^(n) )/(d x) = n x^(n-1)`

`(d t^(-1) )/(d x) = -1 t^(-1-1) = - t^(-2) = (-1)/(t^(2) )`

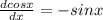
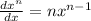
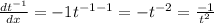
Step(ii):-

Differentiating equation(i) with respective to 't'

`h^(l) (t) = 3(-sin((3\pi )/(2t))(d)/(dt) ((3\pi )/(2t ) )+0` ...(ii)

`h^(l) (t) = 3(-sin((3\pi )/(2t))((-3\pi )/(2t^(2) ) )+0`

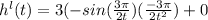
Equating zero

`h^(l) (t) = 3(-sin((3\pi )/(2t))((-3\pi )/(2t^(2) ) )=0`

`3(-sin((3\pi )/(2t))((-3\pi )/(2t^(2) ) ) = 0`

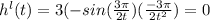
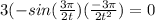
on simplification , we get

`(sin((3\pi )/(2t)) = 0`

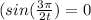
now we use formulas

sin 0 = 0 and sinπ = 0

General solution

`(sin((3\pi )/(2t)) = sin\pi`

`((3\pi )/(2t)) = \pi`

Cancellation 'π' on both sides, we get

`3 = 2 t`

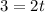
Dividing '2' on both sides , we get

`t = (3)/(2)`

Again differentiating with respective to 't' , we get

`h^(ll) (t) = 3(-cos((3\pi )/(2t))((-3\pi )/(2t^(2) ) )+ (-3)(-sin((3\pi )/(2t) )((6\pi )/(2t^(3) )`

Put t= 3/2 and simplification

`h^(ll) (t) < 0`

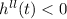
The maximum height

`h(t) = 3 cos ((3\pi )/(2 t) ) +5`

`h((3)/(2) ) = 3 cos ((3\pi )/(2((3)/(2) )) )+5`

`h((3)/(2) ) = 3 cos (\pi )+5 = -3+5 =2`

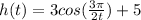
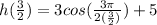
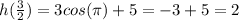
`t = (3)/(2)` seconds elapses between two consecutive times that the swing is at its maximum height 'h' = 2

Conclusion:-

The time
`t = (3)/(2)` seconds elapses between two consecutive times that the swing is at its maximum height 'h' = 2