Answer:
Loading/unloading hourly rate: $70
Packing/unpacking hourly rate: $55
Explanation:
We can write this as a system of linear equations.
We define L as the loading/unloading hourly rate, and P as the packing/unpacking hourly rate.
"One quote was for a weekday move which is for 8 hours of loading/unloading and 6 hours of packing/unpacking for $890":

"The other quote was for a weekend move which is for 5 hours of loading/unloading and 3 hours of packing/unpacking for $515":
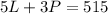
If we express L in function of P in the first equation, and then replace this value in the second equation, we have:
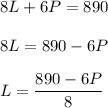
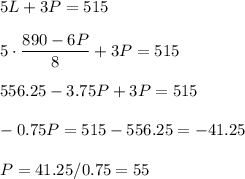
Then, L is:
