Answer: The number of ways of arranging the letters of EQUATION, so that all the vowels are in alphabetical order = 336 .
Explanation:
Given word = "EQUATION"
Total letters = 8
Total Vowels (EUAIO)=5
Total number of ways to arrage letters = 8!
Number of ways to arrange vowels in alphabetical order = 5!
Then, The number of ways that all the vowels are in alphabetical order will be :
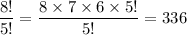
Hence, the number of ways of arranging the letters of EQUATION, so that all the vowels are in alphabetical order = 336 .