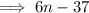Answer:
6n - 37
Explanation:
The derivative of the function f(x) gives the gradient (slope) of the tangent to the graph of y = f(x) at the point (x, y).
Given:

Therefore, the gradient (slope) of the given curve at x is:
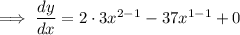
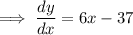
To find the slope, simply substitute x for n: