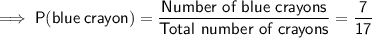Answer:
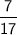
Explanation:
Given information:
- 6 red crayons
- 7 blue crayons
- 4 green crayons
⇒ total number of crayons = 6 + 7 + 4 = 17
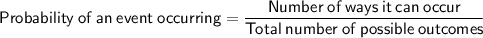
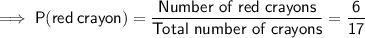
If the red crayon is put back in the bag, the drawing of the red crayon prior to drawing the blue crayon will not affect the probability of drawing a blue crayon.