Question

A 12-centimeter rod is held between a flashlight and a wall as shown. Find the length of the shadow on

the wall of the rod is 45 cm from the wall and 15 cm from the light.

Answer 1

48 cm

Explanation:

Given:

Distance of rod from the wall = 45 cm

Distance of rod from the light = 15 cm

Length of rod = 12 cm

We can see that <DAM and <BAF are equal

Also, <DMA and <BFM are equal because they are corresponding angles

To find the length of the shadow, let's take the equation

`(DM)/(BF) = (AM)/(A.F)`

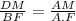
Where.:

DM = ½ of length of the rod = ½*12 = 6

A.F = 15 + 45 = 60 cm

AM = 15 cm

Therefore,

`(DM)/(BF) = (AM)/(A.F)`

`= (6)/(BF) = (15)/(60)`

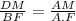
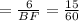
Cross multiplying, we have:

15 * B.F = 60 * 6

15 * B.F = 360

`BF = (360)/(15)`

BF = 24 cm

The shadow on the wall =

2 * BF

= 2 * 24

= 48 cm

The shadow on the wall is 48 cm