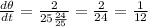Question

A ladder 25 feet long is leaning against the wall of a house. The base of the ladder is pulled away from the wall at a rate of 2 feet per second.(a) What is the velocity of the top of the ladder when the base is given below?7 feet away from the wall ft/sec20 feet away from the wall ft/sec24 feet away from the wall ft/sec(b) Consider the triangle formed by the side of the house, ladder, and the ground. Find the rate at which the area of the triangle is changing when the base of the ladder is 7 feet from the wall. ft2/sec(c) Find the rate at which the angle between the ladder and the wall of the house is changing when the base of the ladder is 7 feet from the wall. rad/sec

Answer 1

a) The height decreases at a rate of
`(7)/(12)` ft/sec.

b) The area increases at a rate of
`(527)/(24)` ft^2/sec

c) The angle is increasing at a rate of
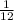`(1)/(12)` rad/sec

Explanation:

Attached you will find a sketch of the situation. The ladder forms a triangle of base b and height h with the house. The key to any type of problem is to identify the formula we want to differentiate, by having in mind the rules of differentiation.

a) Using pythagorean theorem, we have that
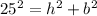`25^2 = h^2+b^2`. From here, we have that

`h^2 = 25^2-b^2`

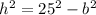
if we differentiate with respecto to t (t is time), by implicit differentiation we get

`2h (dh)/(dt) = -2b(db)/(dt)`

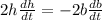
Then,

`(dh)/(dt) = -(b)/(h)(db)/(dt)`.

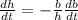We are told that the base is increasing at a rate of 2 ft/s (that is the value of db/dt). Using the pythagorean theorem, when b = 7, then h = 24. So,

`(dh)/(dt) = -(2\cdot 7)/(24)= (-7)/(12)`

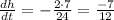
b) The area of the triangle is given by

`A = (1)/(2)bh`

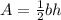
By differentiating with respect to t, using the product formula we get

`(dA)/(dt) = (1)/(2) ((db)/(dt)h+b(dh)/(dt))`

when b=7, we know that h=24 and dh/dt = -1/12. Then

`(dA)/(dt) = (1)/(2)(2\cdot 24- 7(7)/(12)) = (527)/(24)`

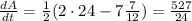
c) Based on the drawing, we have that

`\sin(\theta)= (b)/(25)`

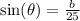
If we differentiate with respect of t, and recalling that the derivative of sine is cosine, we get

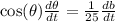`\cos(\theta)(d\theta)/(dt)=(1)/(25)(db)/(dt)` or, by replacing the value of db/dt

`(d\theta)/(dt)=(2)/(25\cos(\theta))`

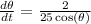
when b = 7, we have that h = 24, then
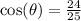`\cos(\theta) = (24)/(25)`, then

`(d\theta)/(dt) = (2)/(25(24)/(25)) = (2)/(24) = (1)/(12)`