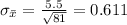Answer:
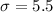
And we have a sample size of n =81. We want to estimate the standard error of the sampling distribution
 and for this case we know that the distribution is given by:
and for this case we know that the distribution is given by:
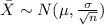
And the standard error would be:
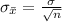
And replacing we got:
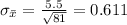
Explanation:
For this case we know the population deviation given by:
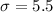
And we have a sample size of n =81. We want to estimate the standard error of the sampling distribution
 and for this case we know that the distribution is given by:
and for this case we know that the distribution is given by:
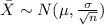
And the standard error would be:
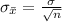
And replacing we got: