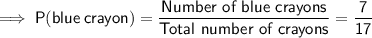Question

Doug has a bag full of crayons. There are 6 red crayons, 7 blue ones, and 4 green crayons. Doug wants to color a blue sky. What is the probability that Doug will pull out a red crayon, put it back in the bag, and then get a blue crayon? Write your answer as a simplified fraction

Answer 1

`\sf (7)/(17)`

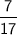
Explanation:

Given information:

• 6 red crayons
• 7 blue crayons
• 4 green crayons

⇒ total number of crayons = 6 + 7 + 4 = 17

`\sf Probability\:of\:an\:event\:occurring = (Number\:of\:ways\:it\:can\:occur)/(Total\:number\:of\:possible\:outcomes)`

`\implies \sf P(red\:crayon) =\frac{\textsf{Number of red crayons}}{\textsf{Total number of crayons}}=(6)/(17)`

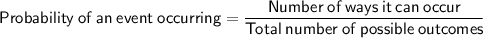
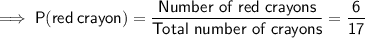
If the red crayon is put back in the bag, the drawing of the red crayon prior to drawing the blue crayon will not affect the probability of drawing a blue crayon.

`\implies \sf P(blue\:crayon)=\frac{\textsf{Number of blue crayons}}{\textsf{Total number of crayons}}=(7)/(17)`