Question

A diameter of a particular circle has endpoints at A(-1, -2) and B(3,10). Which of the following is the

slope of the tangent drawn to this circle at point B?

A) -1/2
B) 4/5
C) -1/3
D) -4

Answer 1

Option C) is correct

Explanation:

Given: Endpoints of the diameter of the circle are A(-1, -2) and B(3,10)

To find: slope of the tangent drawn to the circle at point B

Solution:

Let
`(x_1,y_1)=(-1,-2)\,,\,(x_2,y_2)=(3,10)`

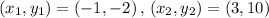
Centre of the circle =
`((x_1+x_2)/(2),(y_1+y_2)/(2))=((-1+3)/(2),(-2+10)/(2))=(1,4)`

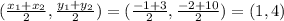
Let
`(h,k)=(1,4)`

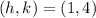
Distance formula states that distance between points (a,b) and (c,d) is given by
`√((c-a)^2+(d-b)^2)`

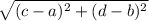
Radius of the circle = Distance between points
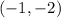`(-1,-2)` and
`(1,4)` =
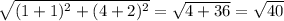`√((1+1)^2+(4+2)^2)=√(4+36)=√(40)` units

Let r =
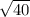`√(40)` units

Equation of a circle is given by
`(x-h)^2+(y-k)^2=r^2`

`(x-1)^2+(y-4)^2=\left ( √(40) \right )^2\\(x-1)^2+(y-4)^2=40`

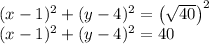
Differentiate with respect to x

`2(x-1)+2(y-4)\frac{\mathrm{d} y}{\mathrm{d} x}=0\\\frac{\mathrm{d} y}{\mathrm{d} x}=(1-x)/(y-4)`

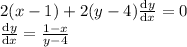
Put
`(x,y)=(3,10)`

`\frac{\mathrm{d} y}{\mathrm{d} x}=(1-3)/(10-4)=(-2)/(6)=(-1)/(3)`

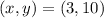
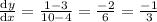
So,

slope of the tangent drawn to this circle at point B =
`(-1)/(3)`