Answer:
Dilation is done by the scale factor of Five-halves.
Explanation:
Please refer to the image attached,
The graph clearly shows the triangles
 ABC and
ABC and
 A'B'C'.
A'B'C'.
Let us calculate the sides of triangles first then we will be able to find scale factor of dilation.
Using the distance formula:
Distance between 2 points
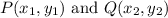 is given by formula:
is given by formula:
PQ =
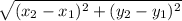
Side AB is along x-axis, side AB =
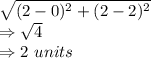
Similarly side, BC = 2 units
Now, in
 A'B'C', A'B' can be calculated by distance formula:
A'B'C', A'B' can be calculated by distance formula:
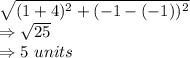
B'C' = 5 units
The ratio of sides:
AB : A'B' = 2:5
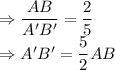
So, scaling factor is
 or 2.5.
or 2.5.
OR
Scaling factor is Five-halves.