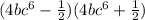Answer:
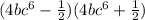
Explanation:
Given
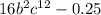
Required
Factor Completely
Follow the steps below;
Rewrite 0.25 as a fraction
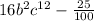
Simplify fraction to lowest term
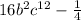
Expand
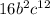
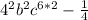
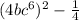
Expand
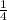
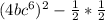
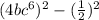
From laws of product of two squares
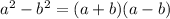
So,
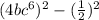 is equivalent to
is equivalent to
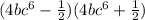
The expression cannot be factorized any further;
Hence, the factor of
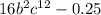 is
is