Question

Among 343 women surveyed, 15 worked the graveyard shift. Among 294 men surveyed, 27 worked the graveyard shift. The samples are independent and were gathered using simple random sampling. Use the critical value method and a 1% significance level to test the claim that the proportion of women working the graveyard shift is less than the proportion of men working the graveyard shift. What is the critical value (rounded to the nearest hundredth)

Answer 1

There is enough evidence to support the claim that the proportion of women working the graveyard shift is less than the proportion of men working the graveyard shift (z=-2.44).

Critical value (α=0.01) zc=-2.33.

Explanation:

This is a hypothesis test for the difference between proportions.

The claim is that the proportion of women (subindex 1) working the graveyard shift is less than the proportion of men (subindex 2) working the graveyard shift.

Then, the null and alternative hypothesis are:

`H_0: \pi_1-\pi_2=0\\\\H_a:\pi_1-\pi_2< 0`

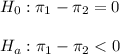
The significance level is 0.05.

The sample 1, of size n1=343 has a proportion of p1=0.0437.

`p_1=X_1/n_1=15/343=0.0437`

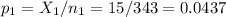
The sample 2, of size n2=294 has a proportion of p2=0.0918.

`p_2=X_2/n_2=27/294=0.0918`

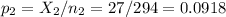
The difference between proportions is (p1-p2)=-0.0481.

`p_d=p_1-p_2=0.0437-0.0918=-0.0481`

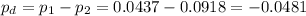
The pooled proportion, needed to calculate the standard error, is:

`p=(X_1+X_2)/(n_1+n_2)=(15+27)/(343+294)=(42)/(637)=0.0659`

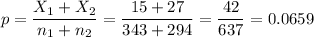
The estimated standard error of the difference between means is computed using the formula:

`s_(p1-p2)=\sqrt{(p(1-p))/(n_1)+(p(1-p))/(n_2)}=\sqrt{(0.0659*0.9341)/(343)+(0.0659*0.9341)/(294)}\\\\\\s_(p1-p2)=√(0.0002+0.0002)=√(0.0004)=0.0197`

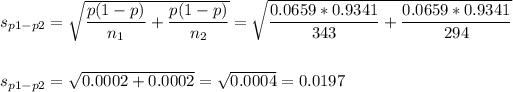
Then, we can calculate the z-statistic as:

`z=(p_d-(\pi_1-\pi_2))/(s_(p1-p2))=(-0.0481-0)/(0.0197)=(-0.0481)/(0.0197)=-2.44`

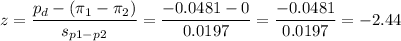
For a significance level of 0.01 and a left-tailed test, the critical value of z is zc=-2.326.

If the test statistic is smaller than the critical value, the null hypothesis is rejected.

The test statistic z=-2.44 is smaller than the critical value zc=-2.326, so the null hypothesis is rejected.

There is enough evidence to support the claim that the proportion of women working the graveyard shift is less than the proportion of men working the graveyard shift.