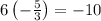Answer: See below
Explanation:
Let us write the equation of the given line in standard form:
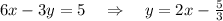
A. The line moves away from the origin by a scale factor of 6, but its inclination still remains the same. Therefore, after any dilation, the slope of that line never changes.
Thus, the slope of the given line after dilation will be the same as the original slope, which is m = 2.
B. The x-intercept of the line before dilation will be given by substituting x = 0 in the given equation as shown below:
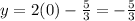
Now, the y-intercept of the line after the dilation will be given by: