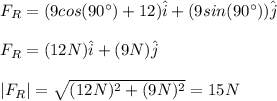Answer:
a) 20.29N
b) 19.43N
c) 15N
Step-by-step explanation:
To find the magnitude of the resultant vectors you first calculate the components of the vector for the angle in between them, next, you sum the x and y component, and finally, you calculate the magnitude.
In all these calculations you can asume that one of the vectors coincides with the x-axis.
a)
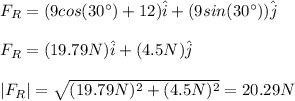
b)
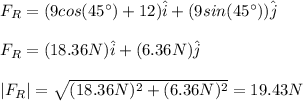
c)