Question

Calculate each probability

given that P(A) = 0.2, P(B)

= 0.8, and A & B are

independent.

Answer 1

Complete question:

Calculate each probability given that P(A) = 0.2, P(B) = 0.8, and A & B are independent.

a) compute P(A and B)

b) If P(A|B) = 0.7, compute P(A and B).

Answer:

(a) P(A and B) = 0.16

(b) P(A and B) = 0.56

Explanation:

Two events are independent if occurrence of one event does not affect possibility of occurrence of another.

(a) if A and B are independent, then P(A and B) = P(A) x P(B)

= 0.2 x 0.8

= 0.16

(b) If P(A|B) = 0.7, compute P(A and B)

Considering the notations of independent events,

`P(A/B) = P(A)\\\\(P(A \ and \ B))/(P(B)) = P(A)\\\\Thus, P(A/B) = (P(A \ and \ B))/(P(B))\\\\P(A \ and \ B) = P(A/B) *P(B)`

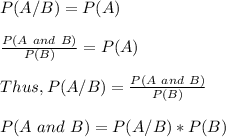
= 0.7 x 0.8

= 0.56