Answer:

Explanation:
The equation of the horizontal hyperbola in standard form is:

The position of its center is:
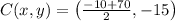
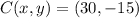
The values for c and a are respectively:
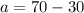
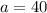
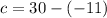

The remaining variable is computed from the following Pythagorean identity:
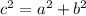

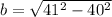

Now, the equation of the hyperbola is:
