Answer:
(A)He only accepts jobs that last 4 or more hours.
Explanation:
Deepak charges $30 for each job plus an additional $15 for each hour he works.
Let the number of hours =x
Deepak's Total Income for x hours =30+15x
Since he only accepts jobs if he will earn at least $90 the job.
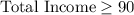

We then solve the inequality for x
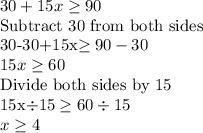
We therefore conclude that Deepak only accepts jobs that last 4 or more hours.
The correct option is A.