Answer:
Z = 0.8528 < 2.576
The calculated value Z = 0.8528 < 2.576 at 0.01 level of significance
Null hypothesis is Accepted at 0.01 level of significance.
There is no significance difference between the means
Step-by-step explanation:
Given data
size of the sample 'n' = 11
mean of the sample x⁻ =20.5
Mean of the Population μ = 18.7
Standard deviation of Population σ = 7
Test statistic

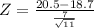
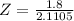
Z = 0.8528
critical Value

The calculated value Z = 0.8528 < 2.576 at 0.01 level of significance
Null hypothesis is Accepted at 0.01 level of significance.
There is no significance difference between the means