Answer:
Explanation:
Since; the density function diagrams were not included in the question; we will be unable to determine the best which depicts this problem.
However;
Let use X to represent the time required for the delivery.
Then X~N(3.8 ,0.8)
i.e
E(x) = 3.8
s.d(x) = 0.8
NOW; P(x>4) = P(X-3.8/0.8 > 4-3.8/0.8)
= P(Z > 0.25)
= 1-P(Z < 0.25)
=1 - Φ (0.25)
= 1 - 0.5987 ( from Normal table Φ (0.25) = 0.5987 )
= 0.4013
Thus; the probability a single delivery would take more than 4 hours is 0.4013
What is the z value corresponding to the interval boundary?
The z value is calculated as:
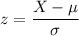
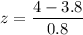
z = 0.25