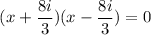Question

What are the solutions to the quadratic equation 9x(2) + 64 = 0?

and
what is the factored form of the quadratic expression 9x(2) + 64?​

Answer 1

Solution of given quadratic equation is

`$ ((8i)/(3), -(8i)/(3) ) $`

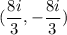
Explanation:

The given quadratic equation is

`9x^2 + 64 = 0`

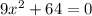
The general form of the quadratic equation is given by

`ax^2 + bx + c = 0`

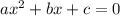
Comparing the general form with the given quadratic equation

`a = 9\\b = 0\\c = 64`

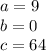
The solutions of the quadratic equation is given by

`$x=(-b\pm√(b^2-4ac))/(2a)$`

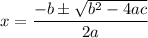
Substitute the values of a, b and c

`$x=(-0\pm√(0^2-4(9)(64)))/(2(9))$`

`$x=(\pm√(-2304))/(18)$`

`$x=(\pm48i)/(18)$`

`$x=(\pm8i)/(3)$`

`$x=(8i)/(3)$`

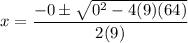
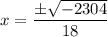
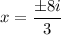
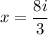
and

`$x=-(8i)/(3)$`

Where i represents iota which means that the given quadratic equation has complex roots.

So the solution of given quadratic equation is

`$ ((8i)/(3), -(8i)/(3) ) $`

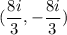
The factored form of the given quadratic equation is

`$ (x+ (8i)/(3)) (x- (8i)/(3)) = 0 $`