Question

Find the area of the triangle QRS, R(6, 10) Q(-9, 5) S(2, -10)

Answer 1

`Area = 140`

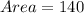
Explanation:

Given

R(6, 10)

Q(-9, 5)

S(2, -10)

Required

Area of triangle RQS

The are of RQS is calculated using the following formula;

`Area = (1)/(2) [R_x(S_y - Q_y) + Q_x(R_y - S_y) + S_x(Q_y - R_y)]`

Where x and y represent the axis of the given coordinates;

Given that R(6, 10);

`R_x = 6 ; R_y = 10`

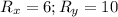
Given that Q(-9, 5);

`Q_x = -9 ; Q_y = 5`

Given that S(2, -10);

`S_x = 2 ; S_y = -10`

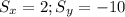
By Substituting these values in the given formula;

`Area = (1)/(2) [R_x(S_y - Q_y) + Q_x(R_y - S_y) + S_x(Q_y - R_y)]`

`Area = (1)/(2) [6(-10 -5) + -9(10 - (-10)) + 2(5 - 10)]`

`Area = (1)/(2) [6(-15) + -9(10 + 10)) + 2(-5)]`

`Area = (1)/(2) [-90 + -9(20)) - 10]`

`Area = (1)/(2) [-90 -180 - 10]`

`Area = (1)/(2) [-280]`

The expression |-280| means absolute value of -280 and the value is 280

`Area = (1)/(2) [-280]`

`Area = (1)/(2)* 280`

`Area = 140`

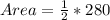
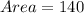
Hence, the area of the triangle is 140