Question

Find the time required for an investment of 5000 dollars to grow to 6100 dollars at an interest rate of 7.5 percent per year, compounded quarterly.

Answer 1

The time (t) = 2.6 years

Explanation:

To calculate the time for earning a compound interest, compounded on a certain amount of present value (PV), compounded periodically, the following formula is used:

`FV=PV(1+(i)/(n) )^(n*t)`

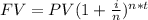
where:

FV = future value = $6,100

PV = present value = $5,000

i = interest rate in decimal = 7.5% = 0.075

n = number of compounding periods per year = quarterly = 4 (4 quarters a year)

t = time of compounding in years = ???

Therefore the time is calculated thus:

`6100=5000(1+(0.075)/(4) )^(4*t)`

`6100=5000(1+0.01875 )^(4t)`

`6100=5000(1.01875 )^(4t)`

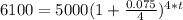
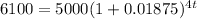
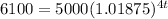
Next, let us divide both sides of the equation by 5000

`(6100)/(5000) = (5000(1.01875)^(4t) )/(5000)`

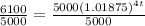
1.22 =
`(1.01875)^(4t)`

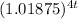
Taking natural logarithm of both sides

㏑(1.22) = ㏑
`(1.01875)^(4t)`

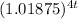
㏑(1.22) = 4t × ㏑(1.01875)

0.1989 = 4t × 0.01858

4t =
`(0.1989)/(0.01858) = 10.71`

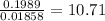
∴ 4t = 10.71

t = 10.71 ÷ 4 = 2.6 years