Answer:
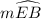 = 96°
= 96°
Explanation:
From the figure attached,
m∠ECB = 25°
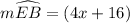 degrees
degrees
 degrees
degrees
From the theorem of secants intersecting outside the circle,
m∠ECB =
![(1)/(2)[m\widehat {DB}-m\widehat{EB}]](https://img.qammunity.org/2021/formulas/mathematics/high-school/3mtgokf8p1eogd2sbxbausof43p9lav8uq.png)
25° =
![(1)/(2)[(7x + 6) - (4x + 16)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/5o20do2e6dka2jk0k0yfjw5ldh740esr7k.png)
25° =
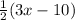
50 = 3x - 10
3x = 60
x =
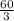
x = 20
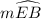 = (4 × 20 + 16)°
= (4 × 20 + 16)°
= (80 + 16)°
= 96°
Therefore, measure of arc EB is 96°.