Answer:
(A) The correct option is (A).
(B) The correct option is (E).
Explanation:
The events can be defined as follows:
X = students felt they learned better at home
Y = students plan on taking an online course in college
The information provided is:
P (X) = 0.24
P (Y|X) = 0.80
P (Y|X') = 0.40
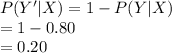
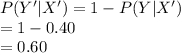
The Bayes' theorem states that the conditional probability of an event E
 given that another event A has already occurred is:
given that another event A has already occurred is:

(A)
Compute the probability a person who does not plan on taking an online course felt they learned better at home as follows:
Use the Bayes' theorem.
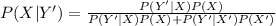
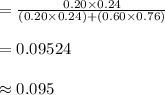
Thus, the probability a person who does not plan on taking an online course felt they learned better at home is 0.095 or 2/21.
(B)
Compute the probability a person who does plan on taking an online course felt they did not learn better at home as follows:
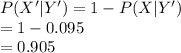
Thus, the probability a person who does plan on taking an online course felt they did not learn better at home is 0.905.