Question

If SinP + SinQ = 7/5 and angle P + angle Q = 90 degrees, without the use of a calculator, determine the value of Sin2P

Answer 1

sin2P ≈ 1

Explanation:

Given SinP + SinQ = 7/5...1 and

∠P + ∠Q = 90°... 2

From compound angle; SinP +SinQ =
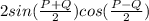`2sin((P+Q)/(2) )cos((P-Q)/(2) )`... 3

Substituting equation 2 into 3 we will have;

SinP +SinQ =
`2sin((90)/(2) )cos((P-Q)/(2) )` = 7/5

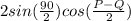`2sin45^(0) cos(P-Q)/(2)=7/5`

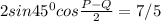
since P = 90-Q from equation 1, then;

`2sin45^(0) cos(90-Q-Q)/(2)=7/5\\2sin45^(0) cos(90-2Q)/(2)=7/5\\2((1)/(√(2) ) ) cos(90-2Q)/(2)=7/5\\cos(90-2Q)/(2) = 7/5* (√(2) )/(2) \\cos(90-2Q)/(2) = (7√(2))/(10)\\(90-2Q)/(2) = cos^(-1) (7√(2))/(10)\\(90-2Q)/(2) = 8.15\\90-2Q = 16.30\\2Q = 90-16.3\\2Q = 73.7\\Q = 36.85^(0) \\\\P = 90-36.85\\P = 53.15^(0)`

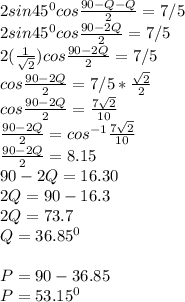
To get sin2P; Accoding to the trig identity;

Sin2P = 2SinPCosP

Sin2P = 2Sin53.15cos53.15

sin2P = 0.9598

sin2P ≈ 1