Question

If the Math Olympiad Club consists of 11 students, how many different teams of 3 students can be formed for competitions?

Answer 1

There will be 3 teams of 3 students, and one team of 2 students, so there will be 4 teams with one team one student short, but only 3 teams that can hold 3 students

Answer 2

165 different teams of 3 students can be formed for competitions

Explanation:

Combinations of m elements taken from n in n (m≥n) are called all possible groupings that can be made with the m elements so that:

• Not all items fit
• No matter the order
• Elements are not repeated

That is, a combination is an arrangement of elements where the place or position they occupy within the arrangement does not matter. In a combination it is interesting to form groups and their content.

To calculate the number of combinations, the following expression is applied:

`C=(m!)/(n!*(m-n)!)`

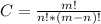
It indicates the combinations of m objects taken from among n objects, where the term "n!" is called "factorial of n" and is the multiplication of all the numbers that go from "n" to 1.

In this case:

• n: 3
• m: 11

Replacing:

`C=(11!)/(3!*(11-3)!)`

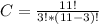
Solving:

`C=(11!)/(3!*8!)`

being:

• 3!=3*2*1=6
• 8!=8*7*6*5*4*3*2*1=40,320
• 11!=39,916,800

So:

`C=(39,916,800)/(6*40,320)`

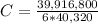
C= 165

165 different teams of 3 students can be formed for competitions