Answer: Both numbers are -11.
Explanation:
You can represent this using two equations, where the variables are x and y:
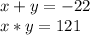
Then, solve the system using substitution by substituting y in the first equation into the second equation:
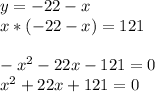
Then, solve the quadratic equation by factoring it:

The only solution (or zero) to the equation is -11.
This means that both numbers are equal to -11.
-11 - 11 = -22
-11 * -11 = 121