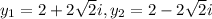Question

Solve the following quadratic equation using the quadratic formula. Separate multiple answers with a comma if necessary.


`−yx^(2) +4y−6=0`

Answer 1

`y^2 -4y +6=0`

`y =(-b \pm √(b^2 -4ac))/(2a)`

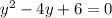
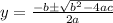
Where
`a = 1, b= -4 ,c =6`

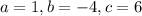
And replacing we got:

`y = (-(-4) \pm √(4^2 -4(1)(6)))/(2*1)`

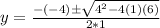
And solving we got:

`y = (4 \pm √(-8))/(2) =2 \pm 2√(2) i`

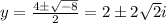
Where
`i =√(-1)`

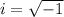
And the possible solutions are:

`y_1=2 + 2√(2) i , y_2 = 2 - 2√(2) i`

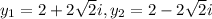
Explanation:

For this case we use the equation given by the image and we have:

`-y^2 +4y -6=0`

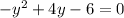
We can rewrite the last expression like this if we multiply both sides of the equation by -1.

`y^2 -4y +6=0`

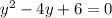
Now we can use the quadratic formula given by:

`y =(-b \pm √(b^2 -4ac))/(2a)`

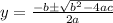
Where
`a = 1, b= -4 ,c =6`

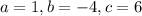
And replacing we got:

`y = (-(-4) \pm √(4^2 -4(1)(6)))/(2*1)`

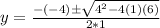
And solving we got:

`y = (4 \pm √(-8))/(2) =2 \pm 2√(2) i`

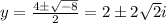
Where
`i =√(-1)`

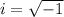
And the possible solutions are:

`y_1=2 + 2√(2) i , y_2 = 2 - 2√(2) i`