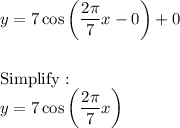Question

Find an equation of cosine function with maximum of 7, minimum of -7 and period of 7

Answer 1

Answer:
`\bold{y=7cos\bigg((2\pi)/(7)x\bigg)}`

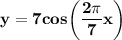
Explanation:

y = A cos (Bx - C) + D

• A = amplitude (vertical stretch)
• Period = 2π/B
• C/B = phase shift
• D = vertical shift

The minimum is -7 and the max is 7 so A = 7 and D = 0

Period is 7. Since P = 2π/B then 7 = 2π/B --> B = 2π/7

Nothing was stated about a phase shift so you can use any value for C. I chose C = 0.

Now, input A = 7, B = 2π/7, C = 0, & D = 0 into the equation

`y=7\cos\bigg((2\pi)/(7)x-0\bigg)+0\\\\\\\text{Simplify}:\\y=7\cos\bigg((2\pi)/(7)x\bigg)`