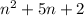Question

1 of 5

What is the nth term rule of the quadratic sequence below?
8, 16, 26, 38, 52, 68, 86,...
Tn=

Answer 1

`n^2+5n+2`

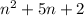
Explanation:

Given the sequence

8, 16, 26, 38, 52, 68, 86,...

The nth term of a quadratic sequence will take the form:

`an^2+bn+c`

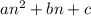
Step 1: Find the difference between each term

The differences are: 8,10,12,14,...

Step 2: Find the differences between the differences

We notice an addition of 2, so the second difference is 2.

Step 3:

Take the half of the second difference to obtain a.

2/2=1

Therefore: a=1

The sequence for now is:
`n^2+bn+c`

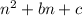
Step 4: Find
`T_n-n^2`

`T_1=8, T_1-1^2=8-1=7\\T_2=16, T_2-2^2=16-4=12\\T_3=26, T_3-3^2=26-9=17`

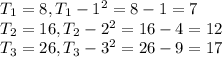
We notice that
`T_n-n^2` forms a linear sequence 7,12,17

We can write this as 2+5n

Therefore, Our nth rule for the quadratic sequence is therefore:
`n^2+5n+2`