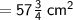Answer:
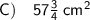
Explanation:
To find the shaded area, subtract the area of the semicircle from the area of the rectangle.
Formulae
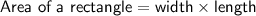
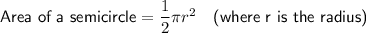
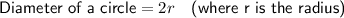
Area of rectangle
Given dimensions of the rectangle:
- width = 7 cm
- length = 11 cm
Substituting these values into the formula:
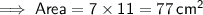
Area of semicircle
Diameter of semicircle = 11 - 2 - 2 = 7 cm
⇒ Radius (r) = 7 ÷ 2 = 3.5 cm
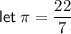
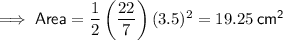
Area of shaded region
= area of rectangle - area of semicircle
= 77 - 19.25
= 57.75