Answer:
AE = 43.2 units
Explanation:
As per the given question image, it can be seen that in the
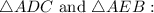
1.
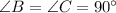
2.
 is common to both the triangles.
is common to both the triangles.
3. Two angles are common, so the third angle
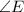 is also equal to
is also equal to
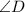 .
.
All the three angles in the
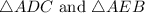 are equal to each other, hence the triangles are similar.
are equal to each other, hence the triangles are similar.
As per the property of similar triangles, the ratio of their sides will be equal.
AB : AC = AE : AD
AC = 88 units
BC = 55 units
AB = AC - AB = 33 units
Let side AE =
 units
units
Side AD = AE + ED
So, AD =
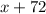
Using the ratio:
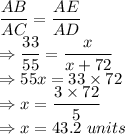
So, AE = 43.2 units