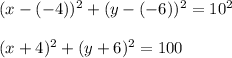Question

Write the equation of a circle centered at the

point P(-4,-6) and passing through the point
R(2,2).

Answer 1

`(x+4)^2+(y+6)^2=100`

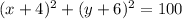
Explanation:

Given a circle centred at the point P(-4,-6) and passing through the point

R(2,2).

To find its equation, we follow these steps.

Step 1: Determine its radius, r using the distance formula

For point P(-4,-6) and R(2,2)

`\text{Distance Formula=}√((x_2-x_1)^2+(y_2-y_1)^2) \\\text{Radius=}√((2-(-4))^2+(2-(-6))^2) \\=√((2+4))^2+(2+6)^2)\\=√(6^2+8^2)\\=√(100)\\Radius=10`

Step 2: Determine the equation

The general form of the equation of a circle passing through point (h,k) with a radius of r is given as:
`(x-h)^2+(y-k)^2=r^2`

Centre,(h,k)=P(-4,-6)

r=10

Therefore, the equation of the circle is:

`(x-(-4))^2+(y-(-6))^2=10^2\\\\(x+4)^2+(y+6)^2=100`