Question

What can you say about the end behavior of the function f(x)=-4x^6+6x^2-52

Answer 1

f(x) = -4x^6 +6x^2-52

The leading coefficient is negative so the left end of the graph goes down.

f(x) is an even function so both ends of the graph go in the same direction.

Answer 2

As x gets smaller, pointing to negative infinity, the value of f decreses, pointing to negative infinity.

As x gets increases, pointing to positve infinity, the value of f decreses, pointing to negative infinity.

Explanation:

To find the end behaviour of a function f(x), we calculate these following limits:

`\lim_(x \to +\infty) f(x)`

And

`\lim_(x \to -\infty) f(x)`

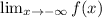
In this question:

`f(x) = -4x^(6) + 6x^(2) - 52`

At negative infinity:

`\lim_(x \to -\infty) f(x) = \lim_(x \to -\infty) -4x^(6) + 6x^(2) - 52`

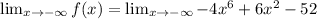
When the variable points to infinity, we only consider the term with the highest exponent. So

`\lim_(x \to -\infty) -4x^(6) + 6x^(2) - 52 = \lim_(x \to -\infty) -4x^(6) = -4*(-\infty)^(6) = -(\infty) = -\infty`

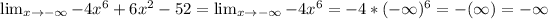
So as x gets smaller, pointing to negative infinity, the value of f decreses, pointing to negative infinity.

Positive infinity:

`\lim_(x \to \infty) f(x) = \lim_(x \to \infty) -4x^(6) + 6x^(2) - 52 = \lim_(x \to \infty) -4x^(6) = -4*(\infty)^(6) = -(\infty) = -\infty`

So as x gets increases, pointing to positve infinity, the value of f decreses, pointing to negative infinity.